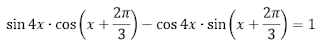Задание.
На рисунках 1 и 2 изображены прямоугольный параллелепипед ABCDA1B1C1D1
с основанием ABCD и
его развертка. Найдите длину ломаной B1D1KB,
если ےC1B1D1=60°,
CD=9 и точки B1,
D1, K
и
B лежат на одной прямой.
Задание.
На рисунках 1 и 2 изображены прямоугольный параллелепипед ABCDA1B1C1D1
с основанием ABCD и
его развертка. Найдите длину ломаной B1D1KB,
если ےC1B1D1=60°,
CD=9 и точки B1,
D1, K
и
B лежат на одной прямой.
Варианты ответов:
1)
27;
2)
27√2;
3)
81√3/2;
4)
12√3+6;
5)
12√3+9.
Теория может пригодиться
Решение
Длину отрезка B1D1
найдем из прямоугольного треугольника B1C1D1,
у которого C1D1=CD=9,
ےC1B1D1=60°
по условию, значит, sin(
ےC1B1D1)=C1D1/B1D1,
откуда B1D1=C1D1/sin ےC1B1D1=9/(√3/2)=18/√3=6√3,
B1C1=3√3
как катет, лежащий против угла в 30°.
Далее, так как точки B1,
D1, K
и
B лежат на одной прямой, то ےAKB=ےC1B1D1=60°
как соответственные при AA1||CB1
и секущей BB1,
а ےAKB=ےD1KA1
как
вертикальные.
Длину D1K
найдем
из прямоугольного треугольника D1KA1,
у него D1A1= B1C1=3√3,
ےD1KA1=60°,
значит sin(
ےA1KD1)=A1D1/KD1,
откуда KD1=A1D1/sin 60°=(3√3)/(√3/2)=6.
Длину BK
найдем
из прямоугольного треугольника BKA, у него AB= CD=9,
ےAKB=60°, значит sin( ےAKB)=AB/KB,
откуда KB=AB/sin 60°=9/(√3/2)=6√3.
Длина ломаной B1D1KB=B1D1+D1K+KB=6√3+6+6√3=12√3+6.
Ответ. 4