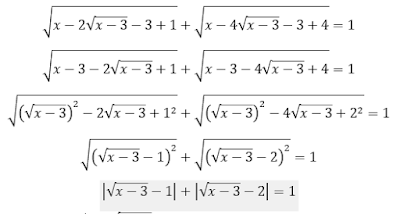Задание. Найдите сумму всех
целых корней уравнения
Теория По иррациональным уравнениям однако настоятельно рекомендую разобрать вот эти Примеры
Анализ. При решении необходимо заметить, что выражения
под знаком корня являются полными квадратами, далее, применяя формулы и
извлекая корень из полного квадрата придем к иррациональному уравнению с
модулем:
Решение
Объединяя решение
получаем, что решением уравнения |t-1|+|t-2|=1 является промежуток [1; 2] или 1≤t≤2. Выполним обратную замену:
Сумма целых значений,
удовлетворяющих этому условию равна 4+5+6+7=22.
Ответ. 22