Построение графиков функций, используя правила преобразования

Изучив соответствующую теорию, приступим к выполнению практических заданий.

Задание: построить график функции:

Самое главное, что необходимо сделать - построить цепочку преобразований функций: от некоторой элементарной функции до необходимой по заданию. И тут - ВНИМАНИЕ! - никакой связи между порядком действий и необходимыми преобразованиями нет! Из правил преобразования видно, что они позволяют нам действовать либо на всю функцию, либо только на аргумент - x, поэтому каждый раз, выполняя преобразование, вы должны спрашивать у себя: "на что я действую - на всю функцию или только на аргумент?".

1. Выбираем элементарную функцию:

Ее график выглядит так:

2. Далее начинаем преобразования. Это может быть модуль, который действует на аргумент или параллельный перенос на 2 единицы вправо, однако во втором случае следующим шагом необходимо будет действовать модулем на x-2, что выполнить нельзя, т.к. действовать можно либо на всю предыдущую функцию, либо только на аргумент. Поэтому вторым преобразованием строим функцию

Правую часть оставляем неизменной и ее же отображаем симметрично влево:

3. А вот теперь можем отнять 2 от аргумента, получим график функции

сдвинув параллельно оси Оx на 2 единицы вправо каждую точку предыдущего графика:

4. Теперь отнимем единицу от всей предыдущей функции: 

Параллельный перенос вдоль оси Oy на 1 единицу вниз: 

5. Действуем модулем на всю функцию:

Часть, которая находится выше оси Ox оставляем неизменной, а часть, которая ниже - отображаем симметрично вверх:

6. Ну и последний шаг, прибавляем 4 ко всей предыдущей функции: 

Поднимаем каждую точку вверх на 4 единицы. Получаем необходимый график: 

Рассмотрим еще один интересный, на мой взгляд, пример: построить график функции 

1. Шаг 1 аналогичен предыдущему примеру: элементарная функция остается та же.

2. Действуем на аргумент в предыдущей функции, отнимая от него единицу:

3. Действуем на аргумент, смотрим на правило построения графика функции y=f(-x)

4. Теперь действуем модулем на аргумент: 

Однако, для построения такого графика, необходимо без изменения оставить ту часть графика, которая располагается правее оси Ох и ее же отобразить симметрично влево, но весь наш график располагается левее оси, что означает, что графика данной функции не существует.

Теперь предлагаю вам самостоятельно построить графики следующих функций:

Преобразования графиков функций.

Профильная программа 10 класса включает в себя такую интересную ему, как преобразования графиков функций. Для начала немного несложной теории.

Будем работать с графиком некоторой функции y=f(x).

• Для того, чтобы получить график функции y=f(x)+b, необходимо каждую точку исходного графика перенести на |b| единиц вверх вдоль оси OY, при b>0 и на |b| единиц вниз вдоль оси OY, если b<0.
• Для того, чтобы получить график функции y=f(x+a), необходимо каждую точку исходного графика перенести на |a| единиц влево вдоль оси OX, при a>0 и на |a| единиц вправо вдоль оси OX, если a<0.
• Для того, чтобы получить график функции y=-f(x), необходимо каждую точку исходного графика отобразить симметрично относительно оси OX.
• Для того, чтобы получить график функции y=f(-x), необходимо каждую точку исходного графика отобразить симметрично относительно оси OY.
• Для того, чтобы получить график функции y=kf(x), необходимо каждую точку исходного графика растянуть в k раз вдоль оси OY, это означает, что из точки (x, y) получится точка (x, ky).
• Для того, чтобы получить график функции y=f(kx), необходимо каждую точку исходного графика сжать в k раз вдоль оси OX, это означает, что из точки (x, y) получится точка (x/k, y).
• Для того, чтобы получить график функции y=\f(x)\, необходимо ту часть графика y=f(x), которая находится на и выше оси OY оставить без изменения, а часть, которая располагается ниже оси OY, отобразить вверх,  симметрично относительно оси OX.
• Для того, чтобы получить график функции y=f(\x\), необходимо ту часть графика y=f(x), которая находится на и правее оси OX оставить без изменения и ее же отобразить симметрично относительно оси OY влево, а часть, которая располагается левее оси OX, не рассматриваем. Внимание! Данная функция всегда будет четная, что очевидно из построения.

А теперь перейдем к практике

Построение сечений многогранников

Всем здравствуйте. Опустим мои поздравления с новым учебным годом и пожелания успехов в учебе. Поступим так же, как поступили учителя 10-х классов: разберем сразу же самую сложную тему не только в 10 классе, но и вообще в школьной математике - более того, любимой всеми геометрии и, в частности, стереометрии. Будет все и сразу.

Изучив аксиомы стереометрии и следствия из них, попробуем построить сечение многогранника.

Итак задача, которую я взяла из 2 этапа репетиционного тестирования прошлого года. Дан куб. Построить сечение плоскостью, проходящей через точки M, N и C, где M - середина ребра A1B1, N - середина ребра AD.

В самом начале нужно обратиться к некоторым понятиям и разграничить четко: чем отличается понятие "грань многогранника" от понятия "плоскость, содержащая грань многогранника", а так же "сечение" от понятия "секущая плоскость".

Грань - это часть плоскости, ограничивающая многогранник, т.е. грань куба - это всегда квадрат, например, грань ABCD, в то время, как плоскость бесконечна и для ее задания достаточно назвать три буквы (обращаемся к первой аксиоме стереометрии). Плоскость, содержащая грань ABCD может быть задана любыми тремя точками, не лежащими на одной прямой, например, плоскость ABC или ACD.

Аналогично разграничим понятия "секущая плоскость" и "сечение".

Плоскость - бесконечна, а сечение - это n-угольник, полученный в результате пересечения секущей плоскости с гранями многогранника. Говоря более простым и понятным языком, сечение - это срез многогранника. Будто разрезать наш многогранник ножом и посмотреть, что получится на срезе. Поэтому для построения сечения необходимо найти прямые, по которым секущая плоскость пересекает плоскости, содержащие грани многогранника и взять отрезки, находящиеся в гранях, концы которых лежат на ребрах многогранника. (Выучите и разберитесь в понятиях ребро, грань и вершина многогранника).

1. Первое, с чем справляется большинство учеников - это найти точки, лежащие в одной плоскости - это точки C и N. Так как обе точки лежат в одной плоскости, то и вся прямая CN лежит в плоскости ABC. Соединяем их. Получаем, что секущая плоскость пересекает плоскость ABC по прямой NC. Тогда отрезок NC - сторона сечения, лежащая в грани ABCD.

И вот здесь многие ученики испытывают самое большое затруднение: а дальше что? Можно ли соединить точки M и N? НЕТ!!! Эти точки не лежат ни в одной из плоскостей, содержащих грань куба, поэтому прямая MN будет лежать в плоскости сечения, но не будет являться стороной сечения, соответственно никак не приблизит нас к решению поставленной задачи.

2. Задаем себе вопрос: в плоскости какой грани лежат прямые, содержащие стороны сечения? Отвечаем: прямая NC лежит в плоскости грани ABCD.

3. Вопрос: какие прямые, содержащие ребра многогранника пересекает эта прямая? Ответ: прямую AB, так как прямые AB и MN лежат в плоскости ABC. Они пересекаются в точке X.

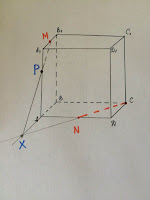
4. Так как точка X принадлежит прямой AB, а прямая AB помимо плоскости ABC, содержится в плоскости ABB1, то точка X так же находится в плоскости ABB1. В плоскости ABB1 по условию. находится точка M, поэтому соединяем эти две точки, так как они лежат в одной грани.  Однако, точка X не содержится в грани ABB1A1, так как выходит за ее границы. Поэтому нас интересует, какая точка будет ограничивать сечение в грани ABB1A1 - это точка пересечения прямой MX с ребром AA1 (они пересекаются, так как лежат в одной плоскости). Построили точку P.

5. Точки P и N лежат в грани ADD1A1, поэтому соединяем их и получаем сторону сечения NP. 

6.Теперь мы снова вернулись к ситуации, когда не знаем как быть дальше, потому что точки M и C не лежат в одной грани, а значит, и соединять их нельзя. Возвращаемся к пункту 2 и задаем себе тот же вопрос: в плоскости какой грани лежат прямые, содержащие стороны сечения? Отвечаем: прямая PM лежит в плоскости грани ABB1A1.

7. Вопрос: какие прямые, содержащие ребра многогранника пересекает эта прямая? Ответ: прямую BB1, так как прямые PM и BB1 лежат в плоскости ABB1. Они пересекаются в точке Y. 

8. Так как точка Y принадлежит прямой BB1, а прямая BB1 помимо плоскости ABB1, содержится в плоскости BCC1, то точка Y так же находится в плоскости BCC1. В плоскости BCC1 по условию. находится точка C, поэтому соединяем эти две точки, так как они лежат в одной грани.  Однако, точка Y не содержится в грани BCC1B1, так как выходит за ее границы. Поэтому нас интересует, какая точка будет ограничивать сечение в грани BCC1B1 - это точка пересечения прямой CY с ребром B1C1 (они пересекаются, так как лежат в одной плоскости). Построили точку Q.

9. Соединяем точки M и Q, так как они находятся в плоскости сечения и обе лежат в грани A1B1C1D1.

10. Получили отрезки пересечения секущей плоскости с каждой из граней куба, значит построили искомое сечение NPMQC.

Кстати, в репетиционном тестировании был вопрос - какая фигура является сечением. И теперь очевидно, что правильный ответ - пятиугольник.