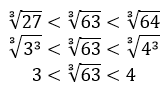До ЦТ осталось совсем мало времени и я надеюсь, что уже все успели зарегистрироваться (если нет, сделайте это в ближайшее время) и теперь ваша подготовка должна свестись к повторению уже изученных тем.
Мы приступили к интегрированным занятиям, когда каждый в своем темпе и по своим темам решает задания, задает вопросы, работает над своими "слабыми местами"
Для тех, кто готовится к тесту и параллельно заглядывает на мой сайт, у меня хорошая новость: за день до теста, утром 17 июня, я выложу свою версию итогового обобщающего теста, который я составила, анализируя задания 2 и 3 этапов репетиционного тестирования, а также демонстрационного теста. Вечером того же дня появятся ответы на него, с которыми можно будет свериться. Я желаю всем сил и терпения, ведь от вас потребуется особенная концентрация и усердие в эти теплые, почти летние дни.
Советую обратить внимание на задания следующего типа и изучить следующую теорию:
Обязательно изучите теорию по многочленам и одночленам (пример в 3 этапе, а во 2 этапе это была вообще Б-часть)
Вспомните, как решаются неравенства (пример в 3 этапе и внимание на Б-часть 3 этапа и Б-часть 2 этапа, а здесь квадратное неравенство из 2 этапа)
Свойства логарифмов (пример в 3 этапе)