Всем хорошего дня и у меня для вас неожиданная новость! Больше ничего изучать не будем!
Нового!
Оставшееся время потратим на систематизацию, повторение и обобщение того, что мы наработали за все время. Кто-то накапливал знания в течение долгих 11 лет, кто-то попытался постигнуть программу всей школьной математики за последний год - при индивидуальной работе с учениками я подстраиваюсь под каждого лично, но с сегодняшнего дня план один для всех: отшлифовываем наши знания!
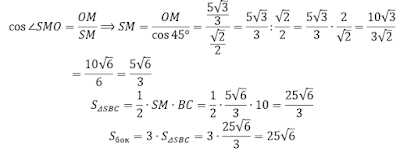
А это значит, что первостепенной задачей для вас теперь является полнейший разбор трех этапов репетиционного тестирования. Практически все задания разобраны здесь. Вы должны не просто просмотреть какого типа задания были, а досконально изучить решение каждого, чтобы у вас не осталось ни вопросов по этим решениям, ни пробелов в теме, по которой это задание.
Далее особое внимание советую обратить на темы, которые переходили из одного этапа в другой:
Мои ученики по каждой из этих тем получат огромное количество заданий для отработки и систематизации. Тем, кто готовится самостоятельно также советую решать много задач на эти темы.
Помимо указанных тем еще решаем в большом количестве:
Преобразования алгебраических выражений и разложение на множители многочленов;
Показательные уравнения;
Геометрические задачи из экзаменационного сборника за 11 класс;
Задачи, связанные с определением и свойствами логарифма;
Упражняемся в переводе единиц измерения
Финальным шагом в подготовке к ЦТ станет, как обычно, составленный мною тест, который я опубликую накануне тестирования.
Всем удачи и сил на оставшиеся полтора месяца, а мы приступаем к такой плотной работе, что даже моя кошка скоро будет готова к сдаче тестирования!