Задание. Длина основания правильной треугольной пирамиды
равна 10, угол между плоскостью основания и боковой гранью равен 45°. Найдите
площадь боковой поверхности пирамиды.
Варианты ответов.
1)
10√6;
2)
25√6;
3)
25√2;
4)
50√3;
5)
50√6.
Теория. Правильная треугольная
пирамида – это такая пирамида, у которой в основании лежит равносторонний
треугольник, а боковые грани являются равными равнобедренными треугольниками.
Решение. Для построения угла на прямой пересечения плоскостей (ребре
основания) необходимо взять точку и построить перпендикуляры к этом ребру в
каждой из плоскостей. Такой точкой может служить M –
середина ребра BC. SM┴BC, так как
треугольник SBC равнобедренный
с основанием BC и M – середина основания, а значит, SM является
не только медианой, но и высотой. Аналогично в равностороннем треугольнике ABC AM является
медианой и высотой (либо по теореме о трех перпендикулярах). Получаем, угол SMA равен 45°.
Sбок=3∙SSBC. По условию длина основания правильной треугольной пирамиды равна 10.
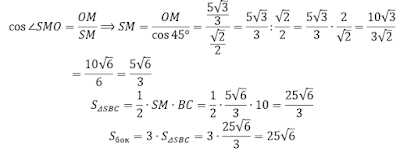
Пусть O – центр треугольника ABC, тогда OM – радиус вписанной окружности и OM=10√3/6=5√3/3.
Ответ. 2


Комментариев нет:
Отправить комментарий