
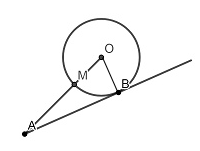
Задание. Из точки A к окружности с центром O проведены касательная AB и отрезок AO. Точки B и M принадлежат окружности
(см. рисунок). Известно, что AB=4√15, AM-MO=3. Найдите длину радиуса окружности.
Варианты ответов.
- 11;
- 4;
- 7;
- 3;
- 15.
Анализ. Так как по условию AM-MO=3, что можно
перефразировать как «AM больше MO на 3. Две величины
неизвестны, однако, связаны соотношением, поэтому удобно меньшую из них взять
за x, то есть MO(радиус)=x, тогда AM=x+3.
Теория. Радиус перпендикулярен
касательной в точке касания.
Решение. Так как O – центр окружности, а точка B принадлежит окружности, то проведем радиус OB и рассмотрим прямоугольный треугольник AOB:
По теореме Пифагора:
AO2=AB2+OB2.
AO=AM+MO=x+(x+3)=2x+3;
OB=OM=x (как радиусы);
AB=4√15 (по условию).
Подставляем в уравнение:
(2x+3)2=(4√15)2+x2;
4x2+12x+9=240+x2;
3x2+12x-231=0
|:3;
x2+4x-77=0
Откуда x=-11 (не подходит) или x=7.
Значит, MO(радиус)=7.
Ответ. 3
Комментариев нет:
Отправить комментарий