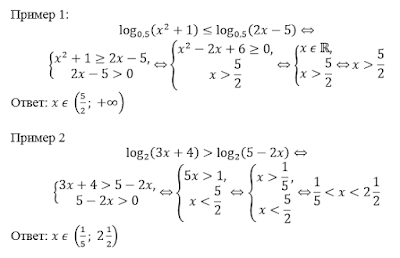Разберем основные способы решения логарифмических неравенств
Смысл решения логарифмических неравенств состоит в том, чтобы перейти путем равносильных переходов к рациональному неравенству или их системе
1. Слева и справа – логарифмы с одинаковым
основанием.
Тогда в зависимости от основания логарифма мы опускаем логарифмы и если
основание больше 1 – оставляем знак неравенства, если основание меньше 1 но
больше 0 – меняем знак неравенства. Вторым неравенством записываем условие
существования меньшего из выражений, стоящих под логарифмом (уже после того,
как логарифмы опустим, смотрим на какое из выражений указывает «носик»
неравенства, то выражение и должно быть больше 0)
2. С одной стороны – логарифм, а с другой число.
Не советую заучивать какие-либо схемы, советую – рассуждать. Из числа
делаем логарифм по тому же основанию, что и исходный логарифм в неравенстве и
дальше поступаем как в пункте 1, однако выставлять ли условие существования
логарифма зависит от того, какое из выражений в неравенстве окажется
наименьшим. Если наименьшее – число, то ставить условие его существования уже
не нужно. (то есть, если вы «снимаете» логарифмы, не забудьте посмотреть на
основание логарифма, нужно ли разворачивать знак неравенства и после этого
оказывается, что «носик» неравенства смотрит на число, то записывать, что это
число больше нуля – уже не нужно).
Если применяем какое-либо свойство логарифма, то обязательно выставляем
условие существования этого (этих) логарифма. Далее действуем как в пунктах 1
или 2, но при переходе от логарифмического уравнения к системе рациональных
условие существования меньшего логарифма уже выставлять не нужно, так как он и
так существует, ведь мы уже ранее выставили это условие
4.
Метод интервалов.
Если из условия понятно, что при переносе в левую часть всех элементов
неравенства, она легко разложится на множители (либо уже разложена на множители
или представляет собой дробь), целесообразно применить метод интервалов
5.
Замена
С заменой в неравенствах советую быть особо
аккуратными и вводить ее только для того, чтобы разложить на множители, а
дальше выполнить обратную замену и решать методом интервалов (как в пункте 4)
Иногда бывает, что все попытки решить
неравенство аналитическими способами не дают должного результата, однако
функции, представленные в неравенстве не являются тяжелыми для построения.
Тогда есть смысл попробовать их изобразить и по рисунку понять, какая из функций
на каком промежутке больше. (не забудем про ОДЗ). Теория по движению графиков
Должны
получится следующие графики:
Асимптота x=1/3
Так как одна функция является возрастающей,
а другая – убывающей, то никаких других точек пересечения у них нет.
Логарифмическая функция ниже (меньше, о чем спрашивали в неравенстве) чем
линейная при
x є (-1; 1/3) – не забудьте ОДЗ!
x є (-1; 1/3) – не забудьте ОДЗ!
Точка пересечения – (-1; 2) – проверьте путем подстановки в
обе функции. Они обе через нее проходят.
Ознакомьтесь с решениями тестовых заданий, предложенных на репетиционном тестировании: