Задание


Решение. SM находим как высоту из треугольника SAB. Сначала находим его площадь по формуле Герона (стороны треугольника 15; 15; 24, значит, полупериметр (15+15+24):2=27):
Теперь подставляем найденное значение в формулу площади треугольника и выражаем оттуда высоту SM:
По формуле Герона ищем площадь:
Выражаем высоту
Ответ. 48

Анализ. При решении задачи очень важно определить, где будет находиться основание высоты пирамиды. Так как ребра SA и SB равны, то ΔSAB - равнобедренный и SM⏊AB, где M - середина стороны AB. Аналогично CM⏊AB, так как ΔCAB также равнобедренный. Значит, высота пирамиды SO будет падать на CM по ттп., то есть O∊СM.
Теория. Объем пирамиды

Площадь треугольника равна полупроизведению стороны на высоту, проведенную к ней.
Площадь треугольника со сторонами a, b и c и полупериметром p, по формуле ГеронаРешение. SM находим как высоту из треугольника SAB. Сначала находим его площадь по формуле Герона (стороны треугольника 15; 15; 24, значит, полупериметр (15+15+24):2=27):
Теперь подставляем найденное значение в формулу площади треугольника и выражаем оттуда высоту SM:
Аналогично высота CM в треугольнике ABC так же равна 9 (он равен треугольнику SAB по трем сторонам, значит и высоты, проведенные к равным сторонам, равны).
Теперь совершенно аналогично находим высоту в треугольнике SMC, она же будет высотой пирамиды.
SM = 9; CM = 9; SC = 12; p = (9+9+12):2=15По формуле Герона ищем площадь:
Выражаем высоту
Все необходимые величины найдены, можем найти объем пирамиды:
В ответ записываем необходимое значение:Ответ. 48


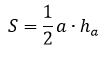







Комментариев нет:
Отправить комментарий