Я не буду вдаваться в подробности, что такое определитель, а перейду сразу к технической стороне вопроса.
Отметим в начале тот факт, что определитель существует только у квадратной матрицы (то есть у матрицы, количество строк и столбцов которой одинаковы).
Для того, чтобы найти определитель матрицы второго порядка (две строки и два столбца), необходимо воспользоваться следующим правилом:
Взять произведение элементов главной диагонали и отнять от них произведение элементов побочной диагонали:
Графически это будет выглядеть так:Приведу пример:
Для нахождения определителя матрицы третьего порядка (три строки, три столбца)
Будем пользоваться правилом треугольников:
Для более легкого запоминания приведу графическую картинку: мы берем произведение элементов (их теперь уже три) главной диагонали и "рисуем" треугольники с основаниями, параллельными этой диагонали, эти элементы будут со знаком "плюс" теперь берем побочную диагональ и треугольники с основаниями, параллельными ей. Эти элементы со знаком "минус", либо вынесем "минус" за скобку
Вот пример
Вообще, нахождение любого определителя лучше проверить - благо в интернете существует огромное количество онлайн калькуляторов. Первым гугл выдал вот этот.
Для нахождения определителей порядков выше третьего, обычно раскрывают его по столбцу или строке. Смысл заключается в следующем: берут любую строку (или столбец) и теперь каждый элемент этой строки (столбца) умножают на -1 в степени, равной сумме порядковых номеров строки и столбца, на месте которых стоял тот элемент, умноженной на определитель, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых стоял данный элемент. Находят сумму полученных произведений.
Например, для нахождения определителя четвертого порядка путем разложения его по второй строке, выполняют следующие преобразования:
Таким образом, определитель будет равенИ далее каждый определитель лучше считать отдельно, а в конце найти сумму.
Например, найдем следующий определитель, разложив его по второй строке:
Отдельно найдем определители:
Результат
Существует еще один способ нахождения определителя матрицы, путем получения с помощью элементарных преобразований (или по правилу прямоугольника) нулей в какой-нибудь строке (столбце). Для этого в интересующей нас строке (разрешающей) выбирают один (любой) элемент, чаще всего равный единице, если такой имеется, и называют его разрешающим элементом. Все остальные элементы этой строки заменяют нулями. Столбец, в котором стоит разрешающий элемент называют разрешающим, и оставляют его без изменения, а все остальные элементы находят по правилу прямоугольника: умножают преобразуемый элемент на разрешающий и вычитают из этого произведения произведение элементов, составляющих вторую диагональ с данными: элемент, стоящий в разрешающей строке и столбце с преобразуемым элементом на элемент, стоящий в разрешающем столбце и строке с преобразуемым элементом.
Покажу наглядно. Допустим, сделаем нули во второй строке. Для этого первый элемент строки будем считать разрешающим (на самом деле вы можете выбрать любой элемент строки), его мы оставляем, а вместо остальных элементов строки записываем нули. Так как разрешающий элемент стоит в первом столбце, то первый столбец будет разрешающим. Элементы разрешающего столбца так же оставляем без изменения.
Все остальные элементы находим по правилу прямоугольников. Для преобразования элемента a12 составляем прямоугольник:И так далее до конца
Теперь можем раскрыть определитель по второй строке, но так как в этой строке только один ненулевой элемент, то раскрывать будем следующим образом:
Для примера найдем определитель этим способом:
Первый элемент второй строки будет разрешающим (что удобно, так как он равен 1), остальные элементы второй строки записываем равными 0, а первый столбец будет разрешающим. Его переписываем без изменения, все остальные элементы находим.
Для элементов первой строкиДля элементов третей строки
Для элементов четвертой строки
Теперь находим определитель, раскрывая его по второй строке.
Ответ получили такой же, как и в первом случае.

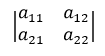




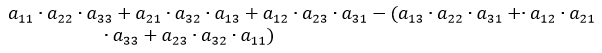




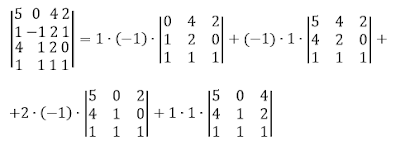










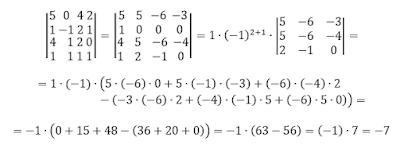
Комментариев нет:
Отправить комментарий