Задание. SABC –
правильная треугольная пирамида, все ребра которой равны 13. Точка M лежит
на ребре SB так,
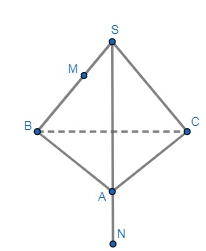
что BM:MS=2:1, NϵSA, NA:AS=1:3 (см.
рис). Найдите длину отрезка, по которому плоскость, проходящая через точки M и N и
параллельная ребру BC,
пересекает основание ABC пирамиды.
Варианты ответов:
Решение
Построим искомый отрезок: соединим точки M и N, так
как они лежат в плоскости ABS.
Пусть отрезок MN пересекает
ребро AB в
точке X.
Проведем через X отрезок
параллельный BC, который пересекает ребро AC в
точке Y. XY –
искомый отрезок. Для его нахождения
необходимо узнать, в каком отношении точка X
разбивает
ребро AB. Для этого проведем прямую MP
в
плоскости ABS (P
–
точка пересечения MP и
SA.
AP:PS=BM:MS=2:1.
SM=SP=MP.
Пусть AN=x, тогда AS=3x,
откуда AP=2x, SP=MP=x.
Рассмотрим подобные треугольники NAX и
NMP,
k=AN:NP=AX:MP,
k=1/3, значит, AX=x/3,
учитывая, что AB=3x, получаем, AX:AB=1:9,
то есть AXY –
равносторонний треугольник со стороной AB/9=13/9= 1 4/9.Ответ. 2
Видео разбор наиболее сложных заданий части а



Комментариев нет:
Отправить комментарий