Сегодня рассмотрим следующую тему: как вносить или выносить множитель из-под знака корня. Именно множитель (!!!) в предыдущей публикации были слагаемые - их никуда выносить нельзя. Я рассмотрю данную тему на примере квадратного корня, однако аналогичные преобразования могут быть выполнены с корнями любой четной степени.
Для начала разберем, что означают записи:
x>0 означает, что переменная x положительна;
x<0 означает, что переменная x отрицательна;
x≥0 означает, что переменная x неотрицательна;
x≤0 означает, что переменная x неположительна.
Никакой знак минус перед переменной не укажет вам на знак переменной! Запись -x>0 является всего лишь линейным неравенством с одной переменной, решая которое (умножаем обе части неравенства на -1, меняем знак неравенства на противоположный), получаем x<0, что говорит о том, что переменная отрицательна.
Вынесение из-под знака корня.
Здесь нам пригодится уже знакомое тождество
Выполняем следующую цепочку преобразований, главная цель которой заключается в том, чтобы у максимального числа множителей под знаком корня выделить вторую степень (т.к. корень второй степени).
И сейчас нам нужно раскрыть знак модуля. С числом вопросов не возникает: |-3|=3, однако с переменной не все так однозначно. Для того, чтобы раскрыть модуль для переменной необходимо воспользоваться определением модуля и узнать, какой знак имеет переменная (положительна или отрицательна). Так как в тексте задания отсутствует условие, накладывающее ограничения на переменную, начинаем искать скрытые подсказки. И тут на помощь нам приходит естественная область определения данного выражения. Так как выражение под корнем всегда неотрицательно, а под корнем у нас остался x, накладываем условие: x≥0, это означает, что x^3≥0, а значит |x^3|=x^3:
Рассмотрим еще один пример:
Здесь нас не интересует знак переменной x, так как применимо равенство:
Теперь о внесении под знак корня.
Пример: внести под знак корня
Так как вносить под корень четной степени можно только неотрицательный множитель, необходимо определить знак выражения -2b. Для этого рассмотрим естественную область определения: b^3≥0, значит b≥0, а значит -2b≤0. Получили, что множитель перед знаком корня отрицательный, поэтому знак минус оставляем перед корнем, внося под корень положительный множитель:
Естественная область определения: -a≥0, значит a≤0, а значит 3a≤0. Множитель перед знаком корня отрицательный, поэтому знак минус оставляем перед корнем, внося под корень положительный множитель:
Естественная область определения: a-5≥0, значит 5-a≤0. Множитель перед знаком корня отрицательный, поэтому знак минус оставляем перед корнем, внося под корень положительный множитель:
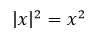
Комментариев нет:
Отправить комментарий