Если вы давно читаете мой блог, то знаете, как ответственно я отношусь к подготовке своих учеников к ЦТ. И я придумала для вас кое-что интересненькое. В марте стартует мой курс экспресс подготовки, ну который вы сможете присоединиться либо в начале марта (весь март работаем над А частью), либо с апреля (добавим Б-часть). За основу я взяла РТ-2 этапа, по каждому заданию подобрала море задач, аналогичных тестовым, записала полезные обучающие видео и готова всем этим с вами поделиться. Все задания буду поверять и комментировать. Так что не упустите возможность попасть ко мне в группу. По поводу стоимости и бронирования места вы можете уточнить на моей странице вконтакте
вторник, 23 февраля 2021 г.
вторник, 26 января 2021 г.
B6. Планиметрия.
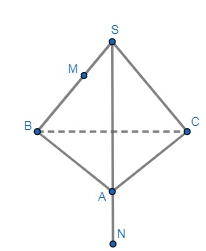
Задание. Биссектриса угла ABC (ﮮABC=60°) пересекает сторону AD в точке H так, что AH:HD=2:1, BH=8. Найдите значение S2, где S – площадь параллелограмма ABCD.
Решение

Ответ. 768
понедельник, 25 января 2021 г.
B5. Тригонометрическое уравнение
Задание. Найдите (в градусах) наибольший отрицательный и наименьший положительный корни уравнения sin 9x∙cos 9°+cos 9x∙sin 9°=-1. В ответ запишите их произведение.
Решение
При n=0,
x=-11
– наибольший отрицательный
При n=1,
x=-11+40=29
– наименьший положительный
Произведение: -11∙29=-319
Ответ. -319
среда, 20 января 2021 г.
B4. Угол между плоскостями
 Пусть CH –
расстояние от точки C до
плоскости β, а CM –
расстояние от точки C до
прямой l. По
определению расстояния CH –
перпендикуляр на плоскость β, CM┴l.
Теорема о трех перпендикулярах: CH –
перпендикуляр, CM –
наклонная MH –
проекция, прямая l перпендикулярна
наклонной, значит, перпендикулярна и проекции.
Пусть CH –
расстояние от точки C до
плоскости β, а CM –
расстояние от точки C до
прямой l. По
определению расстояния CH –
перпендикуляр на плоскость β, CM┴l.
Теорема о трех перпендикулярах: CH –
перпендикуляр, CM –
наклонная MH –
проекция, прямая l перпендикулярна
наклонной, значит, перпендикулярна и проекции. φ – угол между
плоскостями, по определению он равен углу между перпендикулярами к прямой l, то есть между прямыми HM
и
CM,
то есть углу CMH. Треугольник CHM
–
прямоугольный, у которого катет CH в
16 раз меньше гипотенузы CM. Обозначив CH=x,
CM=16x,
по теореме Пифагора MH=x√255, значит, tg φ
– это отношение CH к
MH,
то есть tg
φ
= 1/√255, тогда 1/(tg2
φ)=255.
Ответ. 255
пятница, 15 января 2021 г.
B3. Текстовая задача
Задание. Из спичечного коробка взяли третью часть спичек, в результате в коробке осталось более 27 спичек. Если бы из коробки взяли 22 спички, то их осталось бы меньше половины. Сколько спичек было в коробке первоначально?
Решение
Так как третья часть
спичек должна выражаться натуральным числом, то первоначальное количество
спичек должно делиться на 3. Пусть в коробке было 3x спичек, тогда, после того, как из
коробка взяли третью часть, а это x
спичек,
в коробке осталось 3x-x=2x
спичек.
По условию задачи 2x>27. Если бы из коробка, в котором
лежит 3x спичек, взяли 22 спички, в нем осталось
бы 3x-22. По условию задачи это число больше
половины от 3x, то есть больше 1,5x.
Составим систему неравенств и решим ее.
По смыслу задачи
подходит только натуральное значение x, то есть x=14. Значит, изначально
в коробке было 14∙3=42 спички.
Ответ. 42
четверг, 14 января 2021 г.
вторник, 12 января 2021 г.
B1. Свойства элементарных функций
Задание. Для начала каждого из предложений А – В подберите его окончание 1 – 6 так, чтобы получилось верное утверждение.
РешениеОтвет. А1Б3В6
пятница, 25 декабря 2020 г.
A20. Сечение
Варианты ответов:
Ответ. 2
Видео разбор наиболее сложных заданий части а
A19. Неравенство с модулем
Задание. Найдите сумму всех целых решений неравенства |x2-3x-13|>x2-3x-13
Варианты ответов:
1)
-9;
2)
9;
3)
0;
4)
-12;
5)
12.
Анализ
Обратим внимание, что
выражение под модулем и выражение в правой части – равные многочлены, поэтому
проанализируем, при каких a верно
неравенство |a|>a. Понятно, что нам
нужно рассмотреть случаи, когда a –
отрицательное, положительное и равное нулю. Подставляем любые значения a и
смотрим, верно ли неравенство:
При a=-1: |-1|>-1 – верно;
При a=0: |0|>0 – неверно.
При a=1: |1|>1 – неверно.
Решение
То есть, неравенство
верно, когда под модулем стоит отрицательное выражение, поэтому исходное
неравенство равносильно неравенству
x2-3x-13<0
– квадратное неравенство.
Рассмотрим функцию y= x2-3x-13.
График – парабола, ветви направлены вверх, нули: D=9+4∙13=61. Корни находим приблизительно:
x1=(3-7,8)/2=-2,2;
x2=(3+7,8)/2=5,4.
Строим схематично график:
Решение неравенства xϵ(-2,2; 5,4). Целые значения переменной
-2; -1; 0; 1; 2; 3; 4; 5. Сумма 3+4+5=12.
Ответ. 5