Изучив соответствующую теорию, приступим к выполнению практических заданий.
Задание: построить график функции:
Самое главное, что необходимо сделать - построить цепочку преобразований функций: от некоторой элементарной функции до необходимой по заданию. И тут - ВНИМАНИЕ! - никакой связи между порядком действий и необходимыми преобразованиями нет! Из правил преобразования видно, что они позволяют нам действовать либо на всю функцию, либо только на аргумент - x, поэтому каждый раз, выполняя преобразование, вы должны спрашивать у себя: "на что я действую - на всю функцию или только на аргумент?".
1. Выбираем элементарную функцию:
Ее график выглядит так:
2. Далее начинаем преобразования. Это может быть модуль, который действует на аргумент или параллельный перенос на 2 единицы вправо, однако во втором случае следующим шагом необходимо будет действовать модулем на x-2, что выполнить нельзя, т.к. действовать можно либо на всю предыдущую функцию, либо только на аргумент. Поэтому вторым преобразованием строим функцию
Правую часть оставляем неизменной и ее же отображаем симметрично влево:
3. А вот теперь можем отнять 2 от аргумента, получим график функции
сдвинув параллельно оси Оx на 2 единицы вправо каждую точку предыдущего графика:
4. Теперь отнимем единицу от всей предыдущей функции:
Параллельный перенос вдоль оси Oy на 1 единицу вниз:
5. Действуем модулем на всю функцию:
Часть, которая находится выше оси Ox оставляем неизменной, а часть, которая ниже - отображаем симметрично вверх:
6. Ну и последний шаг, прибавляем 4 ко всей предыдущей функции:
Поднимаем каждую точку вверх на 4 единицы. Получаем необходимый график:
Рассмотрим еще один интересный, на мой взгляд, пример: построить график функции
1. Шаг 1 аналогичен предыдущему примеру: элементарная функция остается та же.
2. Действуем на аргумент в предыдущей функции, отнимая от него единицу:
3. Действуем на аргумент, смотрим на правило построения графика функции y=f(-x)
4. Теперь действуем модулем на аргумент:
Однако, для построения такого графика, необходимо без изменения оставить ту часть графика, которая располагается правее оси Ох и ее же отобразить симметрично влево, но весь наш график располагается левее оси, что означает, что графика данной функции не существует.
Теперь предлагаю вам самостоятельно построить графики следующих функций:

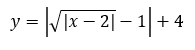





















Комментариев нет:
Отправить комментарий