В прямоугольном треугольнике разность катетов равна 4, а высота, опущенная на гипотенузу, равна 3. Найдите площадь треугольника.

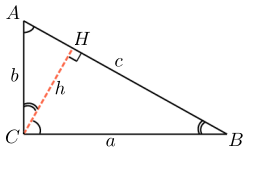
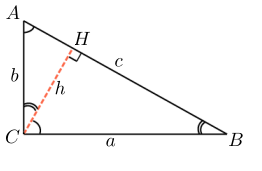
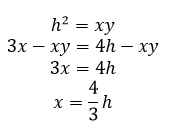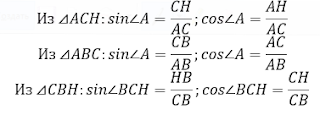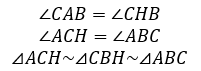 Анализ. Попытки выразить проекции катетов на гипотенузу через неизвестные и связать эти неизвестные теоремой Пифагора, приводят к сложным иррациональным уравнениям либо рациональным уравнениям четвертой степени. Однако интересным оказывается следующее решение.

Решение. Воспользуемся тем, что площадь прямоугольного треугольника можно найти несколькими способами:

Становится очевидным, что AB・CH=AC・CB.

Учитывая, что дана разность катетов, а так же воспользуемся теоремой Пифагора 

произведем следующие преобразования:

Получили квадратное уравнение относительно неизвестной AB. Решая его, по смыслу задачи подходит AB=8. Далее найденное значение гипотенузы подставляем в формулу площади, откуда находим, что площадь треугольника равна 12.

Ответ: 12

Высота прямоугольного треугольника делит его на треугольники с периметрами 3 и 4. Найдите периметр заданного треугольника.

Способ 1.
Анализ. Очевидно, что

Поэтому используя подобие треугольников, выразим через одну переменную стороны и свяжем их, используя данные значения периметров, а так же теорему Пифагора.

Решение. Так как 

то 

Пусть AH=x, BH=y, CH=h, тогда AC=4-(x+y), CB=3-(y+h).

Учитывая, что 

Из треугольника ACH по теореме Пифагора:

Свяжем теперь три стороны, используя периметр и найдем значение h:

Осталось подставить

Ответ: 5.

Способ 2.

Оказывается, что сумма квадратов периметров двух треугольников, на которые высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник, равна квадрату периметра этого треугольника.

Докажем это в общем виде.

Для начала напомню формулу квадрата суммы трех слагаемых:

Рассмотрим треугольники:

Пусть CB=a; AC=b, CH=h, HB=x, тогда AH=c-x. Учитывая, что угол A и угол BCH равны, получаем:

Для удобства в дальнейшем доказательстве я обозначила каждое равенство отдельным цветом. Далее находим сумму квадратов периметров "малых" треугольников:

Теперь, очевидно, для нахождения периметра треугольника необходимо

Ответ: 5.

В прямоугольном треугольнике ABC (угол C - прямой) проведена высота CH. Найдите площадь треугольника, если косинус угла А равен 7/25, а площадь треугольника ACH равна 9,8.

Способ 1.

Анализ. Идея состоит в том, чтобы ввести переменную, выразить через нее все стороны треугольника ACH, используя соотношения сторон в прямоугольном треугольнике, затем найти эту переменную, используя значение площади.

Далее вычислить оставшиеся элементы треугольника ABC и найти его площадь.

Решение.

Рассмотрим треугольник ACH:

Пусть AH = x, тогда:

По теореме Пифагора:

Исходя из формулы площади треугольника:

Находить x нет смысла, так как в задачи необходимо найти площадь треугольника, а это квадратная величина и неизвестная x будет присутствовать в расчетах также во второй степени. Выразим через х гипотенузу AB треугольника ABC, для этого воспользуемся формулой: 

Находим площадь треугольника ABC:

Ответ: 125

Способ 2

Анализ: идея состоит в том, чтобы найти взаимосвязь между формулами площадей треугольников.

Решение: 

Замечаем, что формулы отличаются одним элементом. Теперь необходимо выразить неизвестный нам элемент, гипотенузу AB через AH. Для этого воспользуемся определением косинуса в прямоугольном треугольники (отношение прилежащего катета к гипотенузе).

Из треугольника ACH:

Из треугольника ABC:

Выражаем AB через AH:

Находим площадь треугольника ABC.

Ответ: 125.

Прямоугольный треугольник (теория)

 Рассмотрим формулы, связанные с прямоугольным треугольником.
Сторона, лежащая против прямого угла, называется гипотенузой, две другие стороны - катеты.
1. Соотношения сторон в прямоугольном треугольнике:














2. Любимая теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

3. Если из вершины прямого угла проведена высота (CH), которая делит гипотенузу на отрезки, называемые проекциями катетов на гипотенузу (AH - проекция катета AC, BH - проекция катета CB), имеют место быть формулы:

 Квадрат высоты равен произведению проекций катетов на гипотенузу;

Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.

Отсюда вытекает формула:

Все три треугольника окажутся подобными:

 Радиусы вписанной и описанной окружностей.

Заметим, что центр описанной окружности всегда лежит на середине гипотенузы, поэтому если провести из вершины прямого угла медиану, она будет равна половине гипотенузы.

Площадь можно вычислить следующими способами: