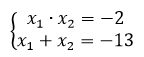Часто в заданиях при
известной сумме (или разности) двух величин требуется найти сумму их квадратов
(кубов, и т.д.), либо же наоборот: известна сумма квадратов, а необходимо найти
сумму (разность) этих величин. Это задания на выделение полного квадрата.
Рассмотрим на примере 1:
найдите
сумму квадратов корней уравнения
По теореме Виета
Сумма квадратов – это выражение
x12+x22
для его вычисления прибавим к этой сумме квадратов их удвоенное произведение и
сразу же вычтем его. Тем самым мы не изменим конечный результат, но проделанные
действия позволят нам свернуть в формулу квадрата суммы первых три слагаемых, а
четвертое слагаемое нам известно по теореме Виета:
Проделываем аналогичные действия: