A2. Углы треугольника

Задание. В равнобедренном треугольнике ABC с основанием AC через вершину B проведена прямая BM, параллельная стороне AC треугольника (см. рисунок). Если градусная мера внешнего угла при вершине A треугольника ABC равна 133°, то градусная мера угла MBC равна. 

Варианты ответов:

1)    65°;

2)    86°;

3)    63°;

4)    43°;

5)    47°.

Теория.

Равнобедренным называется треугольник, две стороны которого равны. Равные стороны называются боковыми, а третья сторона – основание. Углы при основании равнобедренного треугольника, равны. Сумма углов любого треугольника равна 180°.

При пересечении двух параллельных прямых третьей (секущей), образуется 8 углов:

  ے3 и ے6; ے4 и ے5 – внутренние накрест лежащие (равны)

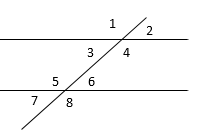
ے3 и ے5; ے4 и ے6 – внутренние односторонние (в сумме дают 180°)

ے1 и ے5; ے2 и ے6; ے3 и ے7; ے4 и ے8 – соответственные (равны)

Внешний угол треугольника – угол, смежный с внутренним. Смежные углы – это углы, у которых одна сторона общая, а две другие образуют развернутый угол. Сумма смежных углов 180°.

Решение.

Так как  градусная мера внешнего угла при вершине A треугольника ABC равна 133°, то по определению внешнего угла и свойству смежных углов, внутренний угол, при вершине A равен 180°-133°=47°. Тогда угол C так же равен 47°, как угол, при основании равнобедренного треугольника. Углы MBC и BCA равны как накрест лежащие при параллельных AC, BM и секущей BC. Получаем, что угол MBC равен 47°.

Ответ. 5