B4, иррациональное уравнение

Задание. Найдите сумму корней (корень, если он единственный) уравнения

В ответ запишите полученный результат, увеличенный в 6 раз.

Теория здесь.

Решение. Так как наше уравнение не является простейшим, очевидно мы не будем вводить замену, то необходимо найти ОДЗ (область допустимых значений) данного уравнения. Она задается следующим образом (каждое подкоренное выражение неотрицательно): 

Так как на множители мы разложить не сможем, то придется возводить обе части в квадрат, однако. Внимание!!! Мы можем это сделать только убедившись, что обе эти части неотрицательные. Так как в левой части мы имеем разность корней, мы не можем сказать, какого знака будет эта часть. Во избежание получения лишних корней, перенесем второе слагаемое из левой части в правую, таким образом получим в левой части выражение под корнем второй степени, которое всегда неотрицательное, а в правой - сумму двух корней второй степени, которая так же будет неотрицательной. Далее имеем право возвести обе части в квадрат.

 Мы получили простейшее уравнение третьего типа (корень равен функции). Можно решать его по правилу, однако я заметила, что для решения этого уравнения правая часть должна быть неотрицательной (так как значение корня всегда число неотрицательное), т.е.

 С учетом нашей ОДЗ получаем единственное число, которое подходит:

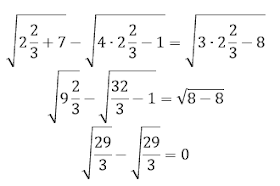
 То есть мы получили решение уравнения (так как в Б-части какой-либо ответ должен существовать). На деле же может оказаться, что это число не является корнем исходного уравнения, поэтому нам необходимо убедиться в правильности решения, подставив это число для проверки в уравнение:

 То есть полученное число действительно является корнем уравнения.

Ответ. 16