Репетитор по математике (Полоцк, Новополоцк): Рациональные неравенства

Для начала вспомним равносильные переходы при решении неравенств (то, что можно делать с любым неравенством).

1. Переносить слагаемое из одной части в другую, меняя знак этого слагаемого;

2. Умножать или делить обе части неравенства на одно и то же, отличное от нуля, число. Причем, если это число отрицательное, необходимо "развернуть" знак неравенства.

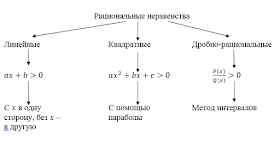
Теперь для дальнейшего решения необходимо определить вид неравенства:

Для решения линейных неравенств слагаемые, в которых есть множитель x переносят в левую часть, слагаемые без x - в правую. Приводят подобные слагаемые в каждой из частей неравенства и делят обе части на коэффициент (множитель перед x), используя правило (2) о равносильных переходах в неравенствах. Полученное решение наносят на числовую прямую и ответ записывают в виде промежутка.

Для решения квадратных неравенств вводят в рассмотрение соответствующую квадратичную функцию и изображают ее схематично. Нас интересует направление ветвей и количество нулей функции. В зависимости от этих критериев получают один из графиков

Далее записывают ответ промежутком в зависимости от условия неравенства.

Метод интервалов для решения дробно-рациональных неравенств применяют только после того, как соблюли все условия в дробно-рациональном неравенстве:

Справа - ноль;
Слева - одна дробь;
И числитель, и знаменатель этой дроби разложены на линейные множители.

Далее вводят в рассмотрение функцию, находят ее область определения и нули, отмечают их на числовой прямой и находят знак функции в каждом промежутке. Особое внимание уделяют нестрогому неравенству. Тогда при ответе не забывают объединять промежутке с нулями функции. Ответ записывают промежутком исходя из знака неравенства в условии.