Способ 1.
Анализ. Идея состоит в том, чтобы ввести переменную, выразить через нее все стороны треугольника ACH, используя соотношения сторон в прямоугольном треугольнике, затем найти эту переменную, используя значение площади.
Далее вычислить оставшиеся элементы треугольника ABC и найти его площадь.
Решение.
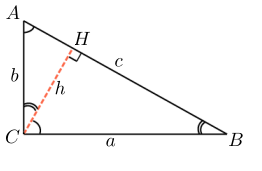
Рассмотрим треугольник ACH:
Пусть AH = x, тогда:
По теореме Пифагора:
Исходя из формулы площади треугольника:
Находить x нет смысла, так как в задачи необходимо найти площадь треугольника, а это квадратная величина и неизвестная x будет присутствовать в расчетах также во второй степени. Выразим через х гипотенузу AB треугольника ABC, для этого воспользуемся формулой:
Находим площадь треугольника ABC:
Ответ: 125
Способ 2
Анализ: идея состоит в том, чтобы найти взаимосвязь между формулами площадей треугольников.
Решение:
Замечаем, что формулы отличаются одним элементом. Теперь необходимо выразить неизвестный нам элемент, гипотенузу AB через AH. Для этого воспользуемся определением косинуса в прямоугольном треугольники (отношение прилежащего катета к гипотенузе).
Из треугольника ACH:
Из треугольника ABC:
Выражаем AB через AH:
Находим площадь треугольника ABC.
Ответ: 125.










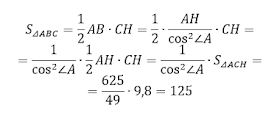
S1/S2=k^2. 9.8/S2=(7/25)^2. S2=625*9.8/49=125
ОтветитьУдалить