Способ 1.
Анализ. Очевидно, что

Анализ. Очевидно, что
Поэтому используя подобие треугольников, выразим через одну переменную стороны и свяжем их, используя данные значения периметров, а так же теорему Пифагора.
Решение. Так как
то
Пусть AH=x, BH=y, CH=h, тогда AC=4-(x+y), CB=3-(y+h).
Учитывая, что
Из треугольника ACH по теореме Пифагора:
Свяжем теперь три стороны, используя периметр и найдем значение h:
Осталось подставить
Ответ: 5.
Способ 2.
Оказывается, что сумма квадратов периметров двух треугольников, на которые высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник, равна квадрату периметра этого треугольника.
Докажем это в общем виде.
Для начала напомню формулу квадрата суммы трех слагаемых:
Рассмотрим треугольники:
Пусть CB=a; AC=b, CH=h, HB=x, тогда AH=c-x. Учитывая, что угол A и угол BCH равны, получаем:
Для удобства в дальнейшем доказательстве я обозначила каждое равенство отдельным цветом. Далее находим сумму квадратов периметров "малых" треугольников:
Теперь, очевидно, для нахождения периметра треугольника необходимо
Ответ: 5.





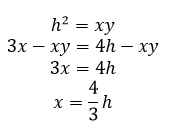



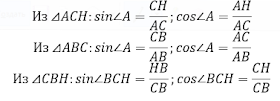



Есть способ проще
ОтветитьУдалитьпредложите, пожалуйста. Задача очень интересная, на мой взгляд
Удалить