Задание. Точка M лежит на оси ординат и равноудалена от точек A(5; 2) и B(-3; 3). Найдите координаты точки M.
Варианты ответов
Решение
Пусть точка M имеет координаты (0; b). Т.к. по условию она принадлежит оси ординат, то ее первая координата будет равна 0. Далее покажем, как составляются расстояния до точек
Расстояние до точки B будет
равно гипотенузе треугольника MBB1 – это прямоугольный
треугольник с катетами MB=|-3|=3 (расстояние по оси Ox
между
точками B и
M
и катет BB1=|3-b| - расстояние по оси Oy
между
точками M и
B.
Аналогично расстояние MA
находим
из прямоугольного треугольника AMA1, где A1M=|5|=5,
AA1=|2-b|.
Эти два расстояния по
условию равны, т.е.
Значит, точка M
имеет
координаты (0; -5 ½)
Ответ. 2

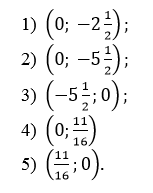


Комментариев нет:
Отправить комментарий