Задание. Найдите произведение наибольшего целого решения на количество целых решений неравенства
Теперь можно приступать к методу интервалов:
Рассмотрим функцию
Теория по теме "рациональные неравенства" здесь .
Анализ Будем внимательны, так как перед нами нестрогое неравенство, это означает, что при записи промежутка, являющегося решением, не забудем включить в него нули функции. Так же в знаменателе дроби записан квадратный трехчлен с отрицательным старшим коэффициентом - не забудем учесть это в разложении на линейные множители знаменателя. В задании говорится о целых решениях, подробнее о числовых множествах здесь.
Решение. Перед нами дробно-рациональное неравенство, так как переменная содержится в знаменателе. Прежде, чем решать его методом интервалов, необходимо проверить три условия:
- Справа действительно стоит ноль
- Слева действительно одна дробь
- Однако ни числитель, ни знаменатель этой дроби не разложены на линейные множители.
Разложим числитель.
Для начала вынесем за скобку общий множитель, а затем выражение, оставшееся в скобке,
разложим по формуле
В знаменателе дроби записан квадратный трехчлен, который разложим по этой же формуле. Не забудем, что в данном случае a = -1.
Теперь можно приступать к методу интервалов:
Рассмотрим функцию
Внимание! Сокращать данную дробь нельзя, иначе мы расширим область определения функции!
Область определения данной функции - все действительные числ за исключением чисел 6 и 8.
Нули функции - 0 и 4.
Наносим на числовую прямую область определения и нули функции и находим знак функции в каждом интервале.
Получаем, что функция неотрицательна на промежутке:
Наибольшее целое решение неравенства 7, а целые решения 0; 4; 5; 7 - то есть количество целых решений 4.
Искомое произведение 7 • 4 = 28
Ответ. 28







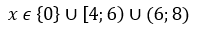
Комментариев нет:
Отправить комментарий