Итак, как же пользоваться таблицей производных сложных функций?
Если вместо функции u мы имеем x, то умножать на x' не нужно, так как x'=1.Функция в данном случае будет простейшая. Например:
Если вместо функции u мы имеем x, то умножать на x' не нужно, так как x'=1.Функция в данном случае будет простейшая. Например:
См. на формулу (5) в таблице.
Теперь возьмем производную сложной функции.
Пользуемся той же самой формулой (5), однако здесь вместо u стоит уже другая, новая функция: arcsin x. Так как это функция, умножать на (arcsin x)' нужно. Для нахождения этой производной смотрим на формулу (11) и на u' не умножаем, так как u=x, то есть функция простейшая.
Если логарифмическая или тригонометрическая функция находится в какой-либо степени, имеет место такая запись:
Однако мы будем понимать, что здесь в третьей степени записана вся функция. И для нахождения ее производной пользуемся формулой (1)
домножаем на u', так как u=sin( e^(x)). и далее до тех пор, пока не получим простейшую функция (u=x).
Теперь решим более сложный пример. Найдем производную функции
Для нахождения производной данной функции, помимо таблицы производных нам понадобятся правила вычисления производных:
Так как мы находим производную суммы двух функций, записываем по правилу пункт 1:
Теперь первое слагаемое - степенная функция пятой степени. Идем слева направо, ищем штрихи и я комментирую нахождение каждого из них (каждой производной). Смотрим в таблице производных (1), а второе слагаемое - дробь. Смотрим в правила пункт 4:
Первая производная представляет сумму двух функций, смотрим правила пункт (1), вторая - снова сумма двух функций, правила пункт (1), третья - корень от некоторой функции, таблица (8):
Первая производна - степень числа e. Таблица (3), вторая - производная натурального логарифма, таблица (5). Третья - производная произведения числа на функцию - правила, пункт (5). Четвертая - производная числа (нет x). Производная числа равна 0! Пятая - производная суммы нескольких функций, правила, пункт (1). Я взяла пятую производную сразу, далее запишу только результат.
Первая производная - смотрим в таблице производную синусов (6), причем функция станет уже простейшей, вторая - производная косинусов. В таблице (7), функция простейшая.
Взяв эти производные, штрихов у нас не осталось, а значит, нахождение производной окончено.


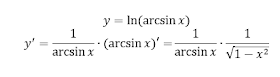

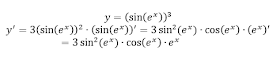







Комментариев нет:
Отправить комментарий