У студентов приближается самая жаркая пора - сессия, а так как ни один студент-заочник экономической специальности не сможет сдать зачет или экзамен по высшей математике, не освоив решение систем линейных уравнений методом Гаусса, разберу сразу на примере.
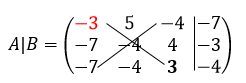
Составим расширенную матрицу системы, выписав коэффициенты переменных в квадратную матрицу 3х3, а через вертикальную черту запишем столбец ответов:
Далее приведем эту матрицу к треугольному виду методом прямоугольника (будем добиваться того, чтобы ниже главной диагонали стояли 0. Берем первый элемент -3, этот элемент будет разрешающим, а стока, в которой он стоит - разрешающей строкой. Ниже разрешающего элемента записываем нули, разрешающую строку оставляем без изменения, а все остальные элементы высчитываем по правилу прямоугольника: умножаем разрешающий элемент на преобразовываемый элемент, таким образом получаем одну диагональ и из произведения вычитаем произведение элементов, которые стоят на другой диагонали. Получим матрицу

Ниже я объясню, каким образом получили эту матрицу:
Чтобы узнать, какой элемент будет стоять на месте -4, составляем разность: умножаем разрешающий элемент (-3) на преобразовываемый (-4) и из произведения вычитаем произведение чисел, одно из которых стоит под разрешающим элементом в преобразовываемой строке (-7), а второе - над преобразовываемым числом в разрешающей строке (5). Итак, (-3・(-4))-(-7・5)=12-(-35)=12+35=47
Чтобы узнать, какой элемент будет стоять на месте 4, составляем разность: умножаем разрешающий элемент (-3) на преобразовываемый (4) и из произведения вычитаем произведение чисел, одно из которых стоит под разрешающим элементом в преобразовываемой строке (-7), а второе - над преобразовываемым числом в разрешающей строке (-4). Итак, (-3・4)-(-7・(-4))=-12-28=-40
Далее поступаем аналогично: (-3・(-3))-(-7・(-7))=9-49=-40
(-3・(-4))-(-7・5)=47
(-3・3)-(-7・(-4))=-37
(-3・(-4))-(-7・(-7))=-37
Теперь разрешающим элементом станет 47, вторая строка - разрешающей. Под этим элементом записываем 0, а остальные находим по правилу прямоугольника и получаем треугольную матрицу:

Ниже объясняю:
(47・(-37))-(47・(-40))=141
(47・(-37))-(47・(-40))=141
Теперь из матрицы записываем систему (коэффициенты переменных записываем перед соответствующими переменными.
Таким образом мы добились того, что из третьего уравнения системы однозначно находится переменная x3:
Подставляем значение найденной переменной во второе уравнение, находим переменную x2:
Подставляем найденные значения переменных в первое уравнение и находим значение переменной x1.
ОТВЕТ: (1; 0; 1).














Комментариев нет:
Отправить комментарий